자연어처리를 위한 행렬연산

이 포스트는 자연어처리에서 사용되는 기본적인 행렬연산에 대해서 이해하는데 목적이 있습니다. 행렬연산에 대해서 알고 계시는 분은 다음 포스트를 참고하세요.

미리 확인해야할 포스트
개발 환경은 google colab을 사용하며 개발 언어는 pytorch를 사용합니다. 이 포스트를 작성할 시점의 pytorch 버전은 1.7.1 입니다.
소스코드
- Colab에서 동작하는 소스코드는 02-01-matrix-equations.ipynb을 참고하시면 됩니다.
- 로컬 컴퓨터에서 동작하는 소스코드는 02-01-matrix-equations.py를 참고하시면 됩니다.
1. 환경
Google colab에서 필요한 환경을 설정하는 과정입니다.
우선 필요한 library를 import 합니다.
1
2
3
4
5
6
import argparse
import random
import matplotlib.pyplot as plt
import numpy as np
import torch
다음은 필요한 환경을 설정합니다.
1
2
3
4
5
6
7
8
9
10
# 환경 설정
args = {
# random seed value
"seed": 1234,
# CPU 또는 GPU 사용여부 결정
"device": torch.device("cuda" if torch.cuda.is_available() else "cpu")
}
args = argparse.Namespace(**args)
print(args)
위 코드의 실행 결과는 아래와 같습니다.
1
Namespace(device=device(type='cpu'), seed=1234)
다음은 random seed를 설정해줍니다.
1
2
3
4
5
# random seed 설정
random.seed(args.seed)
np.random.seed(args.seed)
torch.manual_seed(args.seed)
torch.cuda.manual_seed_all(args.seed)
1. 행렬 A
우선 아래와 같이 실습을 위한 5행 4열의 행렬을 선언합니다. 5행 4열의 행렬의 모양을 $5 \times 4$로 표현합니다.
1
2
3
4
# A 행렬 선언
A = np.random.randint(-9, 10, (5, 4)) / 10
A = torch.tensor(A)
print(A)
위 코드의 실행 결과는 아래와 같습니다. 랜덤 행렬 A가 생성되었습니다.
1
2
3
4
5
tensor([[ 0.6000, -0.3000, 0.3000, 0.6000],
[ 0.8000, 0.0000, 0.2000, 0.3000],
[ 0.7000, -0.4000, 0.7000, 0.0000],
[ 0.6000, 0.9000, 0.7000, 0.3000],
[-0.4000, -0.7000, -0.3000, -0.6000]], dtype=torch.float64)
2. Element Wise Sum
행렬 간의 더하기를 해 보겠습니다. 전제조건은 두 행렬의 모양이 같아야 합니다. 아래 수식과 같이 $m \times n$ 행렬 A와 $m \times n$ 행렬 B의 합은 행렬의 같은 위치의 성분들을 더한 것과 같습니다.
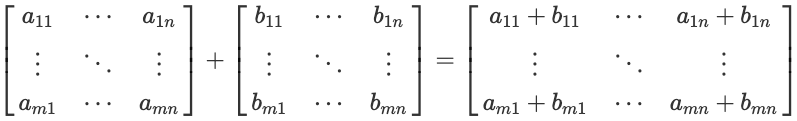
행렬의 합은 교환법칙, 결합법칙이 성립합니다.
- $A + B = B + A$
- $(A + B) + C = A + (B + C)$
행렬의 더하기를 이제 실습으로 확인해 보겠습니다. 우선 A와 더하기를 할 행렬 B를 선언 후 더합니다. 행렬 B도 행렬 A와 같이 $5 \times 4$ 행렬이어야 합니다. 두 행렬의 더히기를 코드로 표현할 때는 $A + B$와 같이 ‘$+$’ 기호를 사용합니다.
1
2
3
4
5
6
7
8
9
# B 행렬 합
B = np.random.randint(-9, 10, (5, 4)) / 10
B = torch.tensor(B)
print(A)
print()
print(B)
print()
print(A + B)
위 코드의 실행 결과는 아래와 같습니다. 행렬의 각 성분들끼리 더해진 것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
tensor([[ 0.6000, -0.3000, 0.3000, 0.6000],
[ 0.8000, 0.0000, 0.2000, 0.3000],
[ 0.7000, -0.4000, 0.7000, 0.0000],
[ 0.6000, 0.9000, 0.7000, 0.3000],
[-0.4000, -0.7000, -0.3000, -0.6000]], dtype=torch.float64)
tensor([[ 0.8000, 0.0000, 0.6000, -0.1000],
[-0.7000, 0.7000, 0.2000, -0.7000],
[ 0.9000, 0.6000, -0.6000, 0.5000],
[-0.7000, -0.5000, -0.8000, 0.1000],
[-0.7000, 0.4000, -0.6000, 0.9000]], dtype=torch.float64)
tensor([[ 1.4000, -0.3000, 0.9000, 0.5000],
[ 0.1000, 0.7000, 0.4000, -0.4000],
[ 1.6000, 0.2000, 0.1000, 0.5000],
[-0.1000, 0.4000, -0.1000, 0.4000],
[-1.1000, -0.3000, -0.9000, 0.3000]], dtype=torch.float64)
2.1. Broadcasting $(m \times n) + (m \times 1)$
다음은 행렬 덧셈에서의 브로드캐스팅에 대해서 알아보겠습니다. 브로드캐스팅은 행령을 더할 때 행 또는 열의 개수가 1일때 자동으로 복사된 성분으로 계산해주는 기능을 말합니다. 자세한 내용은 numpy Broadcasting을 참고하세요.
아래 수식과 같이 $m \times n$ 행렬 A과 $m \times 1$ 행렬 B의 합은 행렬 B의 열을 n번 복사해서 $m \times n$ 행렬로 변경후 행렬의 같은 위치의 성분들을 더한 것과 같습니다.
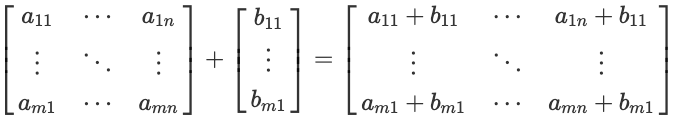
행렬의 브로드캐스팅 더하기를 이제 실습으로 확인해 보겠습니다. 우선 A와 더하기를 할 행렬 B를 선언한 후 더하기를 실행합니다. 이때 행렬 B는 행렬 A와 다르게 $5 \times 1$ 행렬로 선언합니다.
1
2
3
4
5
6
7
8
9
# B 행렬 Boradcasting 합
B = np.random.randint(-9, 10, (5, 1)) / 10
B = torch.tensor(B)
print(A)
print()
print(B)
print()
print(A + B)
위 코드의 실행 결과는 아래와 같습니다. 행렬 B가 브로드캐스팅 후 각 성분들끼리 더해진 것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
tensor([[ 0.6000, -0.3000, 0.3000, 0.6000],
[ 0.8000, 0.0000, 0.2000, 0.3000],
[ 0.7000, -0.4000, 0.7000, 0.0000],
[ 0.6000, 0.9000, 0.7000, 0.3000],
[-0.4000, -0.7000, -0.3000, -0.6000]], dtype=torch.float64)
tensor([[ 0.3000],
[-0.4000],
[ 0.8000],
[ 0.7000],
[-0.1000]], dtype=torch.float64)
tensor([[ 0.9000, 0.0000, 0.6000, 0.9000],
[ 0.4000, -0.4000, -0.2000, -0.1000],
[ 1.5000, 0.4000, 1.5000, 0.8000],
[ 1.3000, 1.6000, 1.4000, 1.0000],
[-0.5000, -0.8000, -0.4000, -0.7000]], dtype=torch.float64)
결과 검증을 위해 pytorch의 repeat 함수를 이용해 행렬 B를 A와 같은 모양으로 열을 복사한 B1 행렬을 이용한 합을 구해봅니다.
1
2
3
4
5
6
# B 행렬 열복사 후 합
B1 = B.repeat(1, 4)
print(B1)
print()
print(A + B1)
위 코드의 실행 결과는 아래와 같습니다. 위 브로드캐스팅 더하기와 결과가 같은것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
tensor([[ 0.3000, 0.3000, 0.3000, 0.3000],
[-0.4000, -0.4000, -0.4000, -0.4000],
[ 0.8000, 0.8000, 0.8000, 0.8000],
[ 0.7000, 0.7000, 0.7000, 0.7000],
[-0.1000, -0.1000, -0.1000, -0.1000]], dtype=torch.float64)
tensor([[ 0.9000, 0.0000, 0.6000, 0.9000],
[ 0.4000, -0.4000, -0.2000, -0.1000],
[ 1.5000, 0.4000, 1.5000, 0.8000],
[ 1.3000, 1.6000, 1.4000, 1.0000],
[-0.5000, -0.8000, -0.4000, -0.7000]], dtype=torch.float64)
2.2. Broadcasting $(m \times n) + (1 \times n)$
두번째 경우는 아래 수식과 같이 $m \times n$ 행렬 A과 $1 \times n$ 행렬 B의 합은 행렬 B의 행을 m번 복사해서 $m \times n$ 행렬로 변경후 행렬의 같은 위치의 성분들을 더한 것과 같습니다.
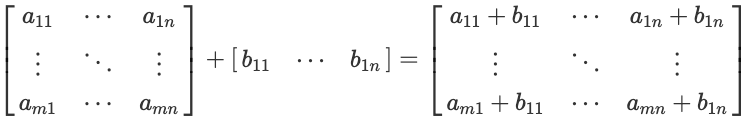
이제 실습으로 확인해 보겠습니다. 우선 A와 더하기를 할 행렬 B를 선언한 후 더하기를 실행합니다. 행렬 B를 행렬 A와 다르게 $1 \times 4$ 행렬로 선언합니다.
1
2
3
4
5
6
7
8
9
# B 행렬 Boradcasting 합
B = np.random.randint(-9, 10, (1, 4)) / 10
B = torch.tensor(B)
print(A)
print()
print(B)
print()
print(A + B)
위 코드의 실행 결과는 아래와 같습니다. 행렬 B가 브로드캐스팅 후 각 성분들끼리 더해진 것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
tensor([[ 0.6000, -0.3000, 0.3000, 0.6000],
[ 0.8000, 0.0000, 0.2000, 0.3000],
[ 0.7000, -0.4000, 0.7000, 0.0000],
[ 0.6000, 0.9000, 0.7000, 0.3000],
[-0.4000, -0.7000, -0.3000, -0.6000]], dtype=torch.float64)
tensor([[0.4000, 0.2000, 0.6000, 0.7000]], dtype=torch.float64)
tensor([[ 1.0000, -0.1000, 0.9000, 1.3000],
[ 1.2000, 0.2000, 0.8000, 1.0000],
[ 1.1000, -0.2000, 1.3000, 0.7000],
[ 1.0000, 1.1000, 1.3000, 1.0000],
[ 0.0000, -0.5000, 0.3000, 0.1000]], dtype=torch.float64)
결과 검증을 위해 pytorch의 repeat 함수를 이용해 행렬 B를 A와 같은 모양으로 행을 복사한 B1 행렬을 이용한 합을 구해봅니다.
1
2
3
4
5
6
# B 행렬 행복사 후 합
B1 = B.repeat(5, 1)
print(B1)
print()
print(A + B1)
위 코드의 실행 결과는 아래와 같습니다. 위 브로드캐스팅 더하기와 결과가 같은것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
tensor([[0.4000, 0.2000, 0.6000, 0.7000],
[0.4000, 0.2000, 0.6000, 0.7000],
[0.4000, 0.2000, 0.6000, 0.7000],
[0.4000, 0.2000, 0.6000, 0.7000],
[0.4000, 0.2000, 0.6000, 0.7000]], dtype=torch.float64)
tensor([[ 1.0000, -0.1000, 0.9000, 1.3000],
[ 1.2000, 0.2000, 0.8000, 1.0000],
[ 1.1000, -0.2000, 1.3000, 0.7000],
[ 1.0000, 1.1000, 1.3000, 1.0000],
[ 0.0000, -0.5000, 0.3000, 0.1000]], dtype=torch.float64)
2.3. Broadcasting $(m \times n) + (1 \times 1)$
두번째 경우는 아래 수식과 같이 $m \times n$ 행렬 A과 $1 \times 1$ 행렬 B의 합은 행렬 B를 복사해서 $m \times n$ 행렬로 변경후 행렬의 같은 위치의 성분들을 더한 것과 같습니다. 이때 B는 행렬이 아닌 실수 스칼라 값이어도 동일합니다.
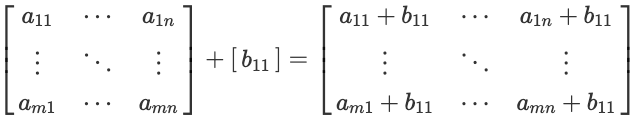
이제 실습으로 확인해 보겠습니다. 우선 A와 더하기를 할 행렬 B를 선언한 후 더하기를 실행합니다. 행렬 B를 행렬 A와 다르게 $1 \times 1$ 행렬로 선언합니다.
1
2
3
4
5
6
7
8
9
# B 행렬 Boradcasting 합
B = np.random.randint(-9, 10, (1, 1)) / 10
B = torch.tensor(B)
print(A)
print()
print(B)
print()
print(A + B)
위 코드의 실행 결과는 아래와 같습니다. 행렬 B가 브로드캐스팅 후 각 성분들끼리 더해진 것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
tensor([[ 0.6000, -0.3000, 0.3000, 0.6000],
[ 0.8000, 0.0000, 0.2000, 0.3000],
[ 0.7000, -0.4000, 0.7000, 0.0000],
[ 0.6000, 0.9000, 0.7000, 0.3000],
[-0.4000, -0.7000, -0.3000, -0.6000]], dtype=torch.float64)
tensor([[-0.9000]], dtype=torch.float64)
tensor([[-0.3000, -1.2000, -0.6000, -0.3000],
[-0.1000, -0.9000, -0.7000, -0.6000],
[-0.2000, -1.3000, -0.2000, -0.9000],
[-0.3000, 0.0000, -0.2000, -0.6000],
[-1.3000, -1.6000, -1.2000, -1.5000]], dtype=torch.float64)
결과 검증을 위해 pytorch의 repeat 함수를 이용해 행렬 B를 A와 같은 모양으로 행을 복사한 B1 행렬을 이용한 합을 구해봅니다.
1
2
3
4
5
6
# B 행렬 행과 열 복사 후 합
B1 = B.repeat(5, 4)
print(B1)
print()
print(A + B1)
위 코드의 실행 결과는 아래와 같습니다. 위 브로드캐스팅 더하기와 결과가 같은것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
tensor([[-0.9000, -0.9000, -0.9000, -0.9000],
[-0.9000, -0.9000, -0.9000, -0.9000],
[-0.9000, -0.9000, -0.9000, -0.9000],
[-0.9000, -0.9000, -0.9000, -0.9000],
[-0.9000, -0.9000, -0.9000, -0.9000]], dtype=torch.float64)
tensor([[-0.3000, -1.2000, -0.6000, -0.3000],
[-0.1000, -0.9000, -0.7000, -0.6000],
[-0.2000, -1.3000, -0.2000, -0.9000],
[-0.3000, 0.0000, -0.2000, -0.6000],
[-1.3000, -1.6000, -1.2000, -1.5000]], dtype=torch.float64)
3. Element Wise Product
행렬 간의 element wise product를 해 보겠습니다. element wise product는 기호로는 $\odot$와 같이 표현합니다. 더하기와 비슷하게 전제조건은 두 행렬의 모양이 같아야 합니다. 아래 수식과 같이 $m \times n$ 행렬 A와 $m \times n$ 행렬 B의 element wise product는 행렬의 같은 위치의 성분들을 곱한 것과 같습니다.
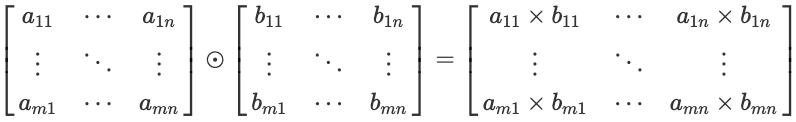
행렬의 element wise product는 교환법칙, 결합법칙이 성립합니다.
- $A \odot B = B \odot A$
- $(A \odot B) \odot C = A \odot (B \odot C)$
행렬의 element wise product를 이제 실습으로 확인해 보겠습니다. 우선 행렬 B를 선언 후 행렬 A와 element wise product를 실행합니다. 행렬 B도 행렬 A와 같이 $5 \times 4$ 행렬이어야 합니다. 두 행렬의 element wise product를 코드로 표현할 때는 $A * B$와 같이 ‘$*$’ 기호를 사용합니다.
1
2
3
4
5
6
7
8
9
# B 행렬 element wise product
B = np.random.randint(-9, 10, (5, 4)) / 10
B = torch.tensor(B)
print(A)
print()
print(B)
print()
print(A * B)
위 코드의 실행 결과는 아래와 같습니다. 행렬의 각 성분들끼리 곱해진 것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
tensor([[ 0.6000, -0.3000, 0.3000, 0.6000],
[ 0.8000, 0.0000, 0.2000, 0.3000],
[ 0.7000, -0.4000, 0.7000, 0.0000],
[ 0.6000, 0.9000, 0.7000, 0.3000],
[-0.4000, -0.7000, -0.3000, -0.6000]], dtype=torch.float64)
tensor([[ 0.8000, -0.9000, 0.8000, 0.0000],
[-0.6000, -0.5000, -0.8000, 0.2000],
[ 0.8000, -0.3000, -0.7000, -0.2000],
[ 0.3000, 0.3000, -0.9000, -0.1000],
[ 0.6000, 0.4000, 0.4000, 0.0000]], dtype=torch.float64)
tensor([[ 0.4800, 0.2700, 0.2400, 0.0000],
[-0.4800, -0.0000, -0.1600, 0.0600],
[ 0.5600, 0.1200, -0.4900, -0.0000],
[ 0.1800, 0.2700, -0.6300, -0.0300],
[-0.2400, -0.2800, -0.1200, -0.0000]], dtype=torch.float64)
3.1. Broadcasting $(m \times n) + (m \times 1)$
다음은 행렬 element wise product에서의 브로드캐스팅은 행열의 더하기와 차이가 앖습니다.
아래 수식과 같이 $m \times n$ 행렬 A과 $m \times 1$ 행렬 B의 합은 행렬 B의 열을 n번 복사해서 $m \times n$ 행렬로 변경후 행렬의 같은 위치의 성분들을 곱한 것과 같습니다.
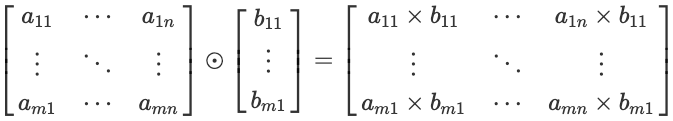
이제 실습으로 확인해 보겠습니다. 우선 행렬 B를 선언한 후 행렬 A와 element wise product를 실행합니다. 이때 행렬 B는 행렬 A와 다르게 $5 \times 1$ 행렬로 선언합니다.
1
2
3
4
5
6
7
8
9
# B 행렬 Boradcasting element wise product
B = np.random.randint(-9, 10, (5, 1)) / 10
B = torch.tensor(B)
print(A)
print()
print(B)
print()
print(A * B)
위 코드의 실행 결과는 아래와 같습니다. 행렬 B가 브로드캐스팅 후 각 성분들끼리 곱해진 것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
tensor([[ 0.6000, -0.3000, 0.3000, 0.6000],
[ 0.8000, 0.0000, 0.2000, 0.3000],
[ 0.7000, -0.4000, 0.7000, 0.0000],
[ 0.6000, 0.9000, 0.7000, 0.3000],
[-0.4000, -0.7000, -0.3000, -0.6000]], dtype=torch.float64)
tensor([[ 0.6000],
[-0.5000],
[-0.2000],
[-0.2000],
[ 0.8000]], dtype=torch.float64)
tensor([[ 0.3600, -0.1800, 0.1800, 0.3600],
[-0.4000, -0.0000, -0.1000, -0.1500],
[-0.1400, 0.0800, -0.1400, -0.0000],
[-0.1200, -0.1800, -0.1400, -0.0600],
[-0.3200, -0.5600, -0.2400, -0.4800]], dtype=torch.float64)
결과 검증은 행렬의 더하기와 차이가 없으므로 생략합니다.
3.2. Broadcasting $(m \times n) + (1 \times n)$
두번째 경우는 아래 수식과 같이 $m \times n$ 행렬 A과 $1 \times n$ 행렬 B의 합은 행렬 B의 행을 m번 복사해서 $m \times n$ 행렬로 변경후 행렬의 같은 위치의 성분들을 곱한 것과 같습니다.
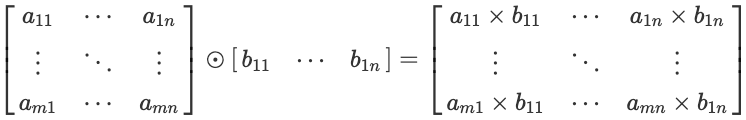
이제 실습으로 확인해 보겠습니다. 우선 행렬 B를 선언한 후 행렬 A와 element wise product를 실행합니다. 행렬 B를 행렬 A와 다르게 $1 \times 4$ 행렬로 선언합니다.
1
2
3
4
5
6
7
8
9
# B 행렬 Boradcasting element wise product
B = np.random.randint(-9, 10, (1, 4)) / 10
B = torch.tensor(B)
print(A)
print()
print(B)
print()
print(A * B)
위 코드의 실행 결과는 아래와 같습니다. 행렬 B가 브로드캐스팅 후 각 성분들끼리 더해진 것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
tensor([[ 0.6000, -0.3000, 0.3000, 0.6000],
[ 0.8000, 0.0000, 0.2000, 0.3000],
[ 0.7000, -0.4000, 0.7000, 0.0000],
[ 0.6000, 0.9000, 0.7000, 0.3000],
[-0.4000, -0.7000, -0.3000, -0.6000]], dtype=torch.float64)
tensor([[-0.2000, 0.9000, -0.4000, -0.7000]], dtype=torch.float64)
tensor([[-0.1200, -0.2700, -0.1200, -0.4200],
[-0.1600, 0.0000, -0.0800, -0.2100],
[-0.1400, -0.3600, -0.2800, -0.0000],
[-0.1200, 0.8100, -0.2800, -0.2100],
[ 0.0800, -0.6300, 0.1200, 0.4200]], dtype=torch.float64)
결과 검증은 행렬의 더하기와 차이가 없으므로 생략합니다.
3.3. Broadcasting $(m \times n) + (1 \times 1)$
두번째 경우는 아래 수식과 같이 $m \times n$ 행렬 A과 $1 \times 1$ 행렬 B의 합은 행렬 B를 복사해서 $m \times n$ 행렬로 변경후 행렬의 같은 위치의 성분들을 곱한 것과 같습니다. 이때 B는 행렬이 아닌 실수 스칼라 값이어도 동일합니다.
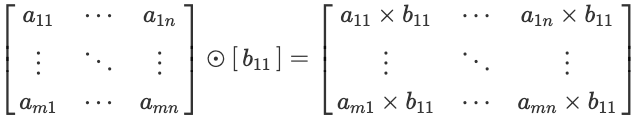
이제 실습으로 확인해 보겠습니다. 우선 행렬 B를 선언한 후 행렬 A와 element wise product를 실행합니다. 행렬 B를 행렬 A와 다르게 $1 \times 1$ 행렬로 선언합니다.
1
2
3
4
5
6
7
8
9
# B 행렬 Boradcasting element wise product
B = np.random.randint(-9, 10, (1, 1)) / 10
B = torch.tensor(B)
print(A)
print()
print(B)
print()
print(A * B)
위 코드의 실행 결과는 아래와 같습니다. 행렬 B가 브로드캐스팅 후 각 성분들끼리 곱해진 것을 확인할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
tensor([[ 0.6000, -0.3000, 0.3000, 0.6000],
[ 0.8000, 0.0000, 0.2000, 0.3000],
[ 0.7000, -0.4000, 0.7000, 0.0000],
[ 0.6000, 0.9000, 0.7000, 0.3000],
[-0.4000, -0.7000, -0.3000, -0.6000]], dtype=torch.float64)
tensor([[-0.8000]], dtype=torch.float64)
tensor([[-0.4800, 0.2400, -0.2400, -0.4800],
[-0.6400, -0.0000, -0.1600, -0.2400],
[-0.5600, 0.3200, -0.5600, -0.0000],
[-0.4800, -0.7200, -0.5600, -0.2400],
[ 0.3200, 0.5600, 0.2400, 0.4800]], dtype=torch.float64)
결과 검증은 행렬의 더하기와 차이가 없으므로 생략합니다.
4. Matrix multiplication
행렬 간의 matrix multiplication를 해 보겠습니다. Matrix multiplication는 기호로는 $A \times B$와 같이 표현합니다. 또는 간단하게 $AB$ 기호를 생락하기도 합니다. 전제조건은 첫 번째 행렬의 열의 개수와 두 번째 행렬의 행의 개수가 같아야 합니다. 아래 수식과 같이 $m \times n$ 행렬 A와 $n \times k$ 행렬 B의 matrix multiplication은 A의 행들과 B의 열들을 dot product 한 것과 같습니다.
결과는 첫 번째 행렬의 행 개수와 두 번째 행렬의 열 개수와 동일한 $m \times k$ 행렬입니다.
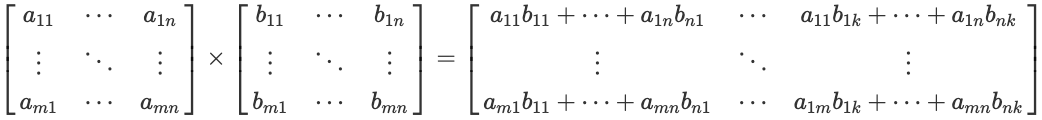
행렬의 matrix multiplication은 교환법칙은 성립하지 않고 결합법칙은 성립합니다.
- $A \times B \ne B \times A$
- $(A \times B) \times C = A \times (B \times C)$
위 행렬을 아래와 같이 행벡터와 열벡터로 표현할 수 있습니다.
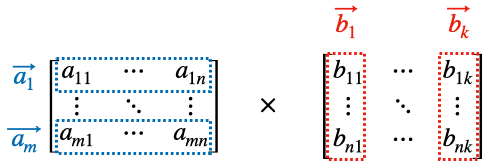
이제 matrix multiplication을 행벡터와 열벡터 수식으로 표현하면 아래와 같습니다.
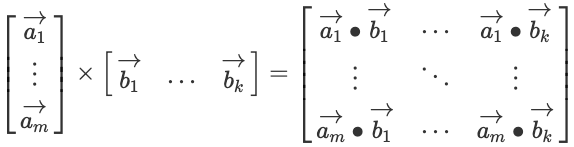
행렬의 matrix multiplication을 실습으로 확인해 보겠습니다. 우선 행렬 B를 선언 후 행렬 A와 matrix multiplication을 실행합니다. 행렬 B의 행은 행렬 A의 열과 같아야 하고 행렬 B의 열은 아무 값이나 주어도 됩니다. 다음과 같이 $4 \times 3$ B 행렬을 선언합니다. 두 행렬의 matrix multiplication은 pytorch의 matmul 함수를 이용해서 구합니다.
1
2
3
4
5
6
7
8
9
# B 행렬 matrix multiplication
B = np.random.randint(-9, 10, (4, 3)) / 10
B = torch.tensor(B)
print(A)
print()
print(B)
print()
print(torch.matmul(A, B))
위 코드의 실행 결과는 아래와 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
tensor([[ 0.6000, -0.3000, 0.3000, 0.6000],
[ 0.8000, 0.0000, 0.2000, 0.3000],
[ 0.7000, -0.4000, 0.7000, 0.0000],
[ 0.6000, 0.9000, 0.7000, 0.3000],
[-0.4000, -0.7000, -0.3000, -0.6000]], dtype=torch.float64)
tensor([[-0.3000, -0.1000, 0.8000],
[ 0.0000, 0.6000, 0.2000],
[ 0.3000, -0.6000, 0.1000],
[ 0.2000, -0.7000, -0.1000]], dtype=torch.float64)
tensor([[ 3.0000e-02, -8.4000e-01, 3.9000e-01],
[-1.2000e-01, -4.1000e-01, 6.3000e-01],
[-1.3323e-17, -7.3000e-01, 5.5000e-01],
[ 9.0000e-02, -1.5000e-01, 7.0000e-01],
[-9.0000e-02, 2.2000e-01, -4.3000e-01]], dtype=torch.float64)
결과 검증을 위해 A의 행벡터와 B의 열벡터의 dot product를 pytorch이 dot 함수를 이용해 직접 구해보겠습니다.
1
2
3
4
5
6
7
# 직접계산
result = torch.zeros(A.size(0), B.size(-1))
for row in range(A.size(0)):
for col in range(B.size(-1)):
result[row][col] = torch.dot(A[row], B[:, col])
print(result)
위 코드의 실행 결과는 아래와 같습니다. pytorch의 matmul의 결과와 동일한 것을 확인할 수 있습니다.
1
2
3
4
5
tensor([[ 0.0300, -0.8400, 0.3900],
[-0.1200, -0.4100, 0.6300],
[ 0.0000, -0.7300, 0.5500],
[ 0.0900, -0.1500, 0.7000],
[-0.0900, 0.2200, -0.4300]])
4.1. 열벡터 연산으로의 해석
딥러닝에서 수식으로 모델을 설명할 때 열벡터로 표현하는 경우가 대부분입니다. 위 행벡터와 열벡터의 수식을 열벡터로 표현하면 아래와 같습니다. A 행렬과 B의 열벡터들의 matrix multiplication으로 표현할 수 있습니다.
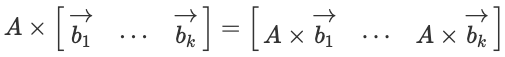
행렬과 하나의 열벡터의 matrix multiplication은 다음과 같이 표현할 수 있습니다.
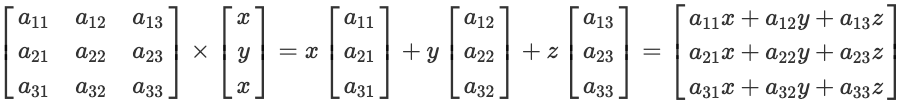
4.2. 행벡터 연산으로의 해석
드물지만 딥러닝에서 수식으로 모델을 설명할 때 행벡터로 표현하는 때도 있습니다. 위 행벡터와 열벡터의 수식을 행벡터로 표현하면 아래와 같습니다. A의 행벡터와 행렬 B의 matrix multiplication으로 표현할 수 있습니다.
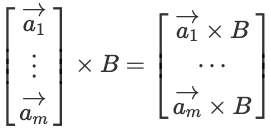
하나의 행벡터와 행렬의 matrix multiplication은 다음과 같이 표현할 수 있습니다.
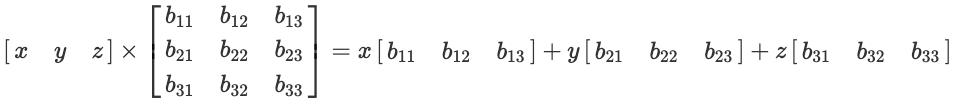
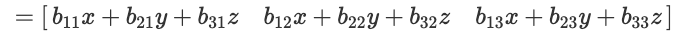
5. Dot Product
두 벡터간의 dot product에 대해서 알아보겠습니다. Dot product의 기호는 $\vec{a} \bullet \vec{b}$와 같이 표현합니다. 전제조건은 두 벡터의 차원 수가 같아야 합니다. 아래 수식과 같이 같은 위치의 성분들을 곱해서 전체를 더한 것과 같습니다. 결과는 하나의 스칼라 값입니다.
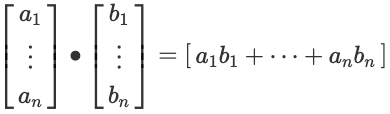
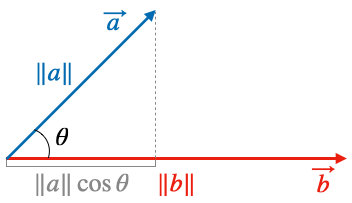
두 벡터의 dot product를 기하적으로 표현하면 다음과 같습니다. 두 벡터의 길이의 곱에 두 벡터가 이루는 내각 $\theta$에 cosine을 취한 값을 더하는 것입니다.
위 그림을 수식으로 표현하면 다음과 같습니다.
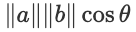
cosine 값은 아래그림과 같이 변합나다.
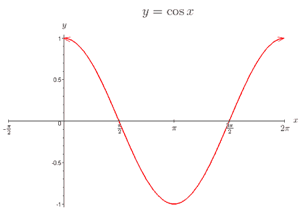
- 두 벡터의 방향이 같을 때 cosine 값이 1이 되어 dot-product 값이 최대가 됩니다
- 두 벡터의 방향이 직각을 이룰 때 cosine 값이 0이 되어 dot-product 값이 0이 됩니다. 이때를 직교(orthogonality) 한다고 표현합니다.
- 두 벡터가 방향이 반대 방향일 때 cosine 값이 -1이 되어 dot-product 값이 최소가 됩니다.
즉 “dot-product의 결과는 두 벡터가 얼마나 유사한지를 비교할 수 있는 기준으로 사용할 수 있습니다.”
벡터의 dot product를 실습으로 확인해 보겠습니다. 우선 두개의 벡터를 선언합니다.
1
2
3
4
5
6
7
8
9
10
# a, b 벡터 선언
a = np.random.randint(-9, 10, (5,)) / 10
a = torch.tensor(a)
b = np.random.randint(-9, 10, (5,)) / 10
b = torch.tensor(b)
print(a)
print()
print(b)
위 코드의 실행 결과는 아래와 같습니다. 두 개의 벡터가 생성되었습니다.
1
2
3
tensor([-0.8000, 0.5000, -0.5000, 0.1000, -0.6000], dtype=torch.float64)
tensor([ 0.8000, 0.6000, -0.9000, 0.4000, 0.7000], dtype=torch.float64)
다음은 pytorch이 dot 함수를 이용해 dot-product를 구합니다.
1
2
# dot-product
print(torch.dot(a, b))
위 코드의 실행 결과는 아래와 같습니다. dot product의 결과인 스칼라값을 확인할 수 있습니다.
1
tensor(-0.1600, dtype=torch.float64)
결과 검증을 위해 두 벡터를 element wise product 값을 구한 후 합을 구해봅니다.
1
2
3
4
5
6
# element wise product and sum
c = a * b
print(c)
print()
print(torch.sum(c))
위 코드의 실행 결과는 아래와 같습니다. 위 dot product와 결과가 같은 것을 확인할 수 있습니다.
1
2
3
tensor([-0.6400, 0.3000, 0.4500, 0.0400, -0.4200], dtype=torch.float64)
tensor(-0.2700, dtype=torch.float64)
지금까지 기본적인 행렬연산에 대해서 알아봤습니다.
